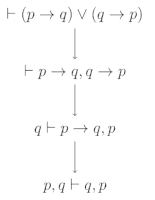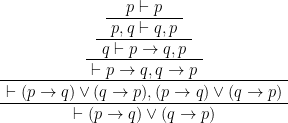ノート: 情報科学における論理①
小野寛晰『情報科学における論理』の読書ノート。なるべく練習問題も解いてく。
2021-11-07 読み返してて気になる点があったので一部を訂正
第1章 命題論理
古典命題論理の形式体系LK
式
式(sequent)は次の形式によって表現される。
ここで は論理式を表す。
上の式は直感的には を仮定すると
が導かれることを意味する。なお
は仮定なしで
が導かれること、
は
を仮定すると矛盾が導かれることをそれぞれ意味する。
推論規則
前提となるいくつかの命題から別の命題を導き出す為の規則を推論規則(inference rule)という。
LKは式から式を導き出す推論規則として以下を備える。なお は論理式、
は長さ0以上の論理式の列を表す。
- Weakening Left (WL)
- Weakening Right (WR)
- Contraction Left (CL)
- Contraction Right (CR)
- Exchange Left (XL)
- Exchange Right (XR)
- Cut
※直感的には三段論法と同じ(と
が空の場合で考えると分かりやすい)
- ∧ Left 1 (∧L1)
- ∧ Left 2 (∧L2)
- ∧ Right (∧R)
- ∨ Left (∨L)
- ∨ Right 1 (∨R1)
- ∨ Right 2 (∨R2)
- → Left (→L)
- → Right (→R)
- ¬ Left (¬L)
- ¬ Right (¬R)
推論規則の上下の式をそれぞれ上式、下式という。
証明図
公理となる式に推論規則を0回以上適用して式 にまで達したとき、
は証明可能(provable)であるといい、その過程を記したものを
に到る証明図(proof figure)という。公理となる式をこの証明図の始式(initial sequent)といい、また
をこの証明図の終式(end sequent)という。
LKは始式として を採用する。
例)ド・モルガンの法則 の証明
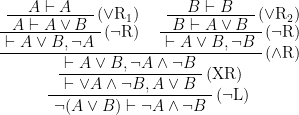
トートロジーな式
論理式に対する性質であるトートロジーを式にも適用できるよう拡張する。
論理式の列 に対して論理式
を次のように定める。
式 がトートロジーであることと、論理式
がトートロジーであることは同じであるとする。
健全性と完全性
LKは健全かつ完全。すなわちLKで証明可能な任意の式はトートロジーであり、任意のトートロジーな式はLKで証明可能。
Cut除去定理
LKで証明可能な式について、推論規則Cutを一度も使わずに証明する証明図が存在する。
Cutが除去できると何が嬉しいのかいまいち分からない……。
終式から証明図を上に辿っていく場合、Cutが含まれていると新しい論理式が突如登場することになる。これは推論規則Cutによる上式が一意に定まらないということであり、機械的操作で証明を行うのが難しい。幸いLKはCutを使わずとも証明能力が変わらない。
練習問題
問1.1
不正。付値
を仮定すれば
となり
が充足不可能でも設問の前提を満たす。
正。
が充足不可能であると仮定する。設問よりすべての付値
に対して
であるがこれを満たすには
でなくてはならない。これは
が充足可能であるという前提に反する。よって
は充足可能。
問1.2
問1.3
論理結合子として のみを含む論理式をBNFで表すと次の通り。ここで
は任意の命題変数を表すものとする。
論理式 がともに真のとき論理式
はいずれも真。従って
によって表現されるすべての命題変数が真のとき論理式
はあきらかに真となる。よって充足可能。
問1.5
問1.7
■ の場合
また
よって任意の付値 について
が成り立つ。
■ の場合
また
よって任意の付値 について
が成り立つ。
■ の場合
同様にして
よって任意の付値 について
が成り立つ。
問1.8
問1.10
面倒臭いので積和形だけ。
問1.11
は
として定義可能。
問1.12
🤔
問1.14
イ.
ロ.
ハ.
①. →L
②. ¬L
③. ∧L2
④. ∧L1
⑤. CL
問1.15
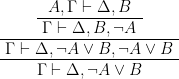
問1.16
1)
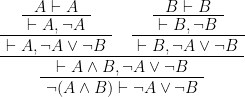
2)
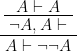
3) 上の左右逆ver.
4)
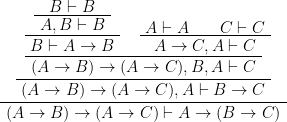
5)
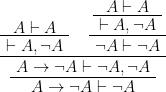
問1.17
1)
![]()
2)
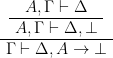
問1.19